1. 분포 시각화
(1) 분포 시각화 정의
데이터의 분포를 시각적으로 표현하는 기법을 말하며, 특정 변수의 값들이 어떻게 분포되어 있는지를 파악하기 위해 사용한다.
- 원그래프와 같이 비율로 영역을 표현하는 경우 각 영역을 모두 합치면 1 또는 100%가 되는 특징을 가진다.
- 분포 데이터의 시각화는 최대, 최소, 전체분포를 나타내는 그래프로 표현하며, 전체의 관점에서 각 부분이 차지하는 정보를 히스토그램, 파이차트, 도넛차트, 누적막대그래프, 트리맵 등으로 시각화한다.
※ 시각화 방법들의 장단점을 구분하자.
(2) 히스토그램(Histogram)
막대그래프의 일종으로 세로축은 데이터의 분포 정도를 표현하고, 가로축은 특정 변수의 구간 폭을 의미한다.
- 데이터셋 안에서 특정 변수의 값이 어떻게 분포되어 있는지를 파악해야 하는 경우(도수분포) 주로 사용한다.
- 도수분포표 : 데이터 값의 다양한 산출 분포를 보여주는 목록이나 표이다. 일정한 범위를 기준(계급이라고 함)으로 데이터 값의 발생 건수를 요약해서 보여준다.
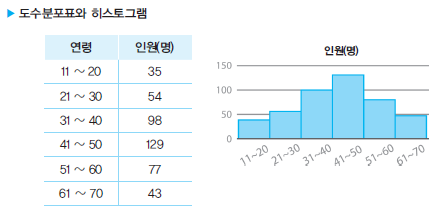
- 구간을 설정해서 데이터를 표현하기 때문에, 적절한 구간 폭을 선택하고 각각의 막대가 동일한 폭을 갖도록 설정해야 시각적으로 정확하게 표현된다.
- 구간폭을 좁게 하는 경우 데이터 분포 차이를 잘 표현할 수 있지만 전체적인 흐름을 파악하기 어려울 수 있고, 구간폭을 넓게 하는 경우는 데이터 분포의 급격한 변화를 표현하기가 어렵다.
- 누적히스토그램(Cumulative Histogram)은 히스토그램의 각 구간의 값을 누적시켜서 표현한다. 따라서, 데이터의 출현 빈도를 오른쪽으로 누적하면서 표시하며 마지막 막대는 전체 데이터의 총 수를 나타낸다.

(3) 원그래프(파이차트)
하나의 원을 구성하는 데이터의 비율에 따라 조각으로 나누어서 데이터의 분포를 표현한다.
- 원을 구성하는 각각의 요소의 비율을 한눈에 보여주지만, 막대그래프와 같이 데이터의 값을 정확하게 표현하기 어렵다는 단점이 있다.
- 하나의 분류에 대한 값의 분포를 표현하기 때문에, 여러 분류에 대한 값을 표현하기 위해서는 각각의 차트가 필요하다.

(4) 도넛차트
막대그래프를 누적하고 도넛 모양으로 만든 형태이며, 원그래프가 면적으로 분포비율을 표현하는데 반해 도넛차트는 면적이 아닌 길이로 데이터 값의 정도를 표현한다.
- 같은 성격의 데이터인 경우 여러 개의 차트를 겹쳐서 보여줄 수 있다.
- 중첩도넛차트 : 도넛차트 여러 개를 겹쳐서 표현하는 것으로, 여러 분류에 대한 값을 하나의 차트로 표현할 수 있다.

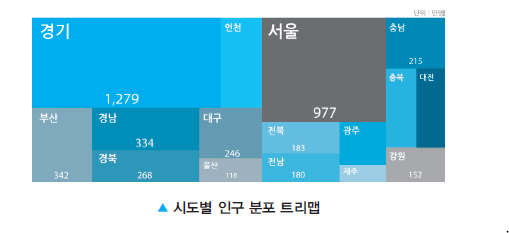
(5) 트리맵
트리맵은 전체 데이터를 표현하는 하나의 사각형 영역에 세부 사각형들의 크기로 데이터의 분포를 시각화하여 표현한다.
- 하나의 대분류에 속한 세부 분류 데이터들의 분포를 영역의 크기를 이용하여 효과적으로 보여준다.
- 내부의 사각형도 하위 분류를 적용해서 다시 맵을 구성할 수 있기 때문에, 계층형/트리 구조를 가진 데이터를 표현하는 데 유용하다.
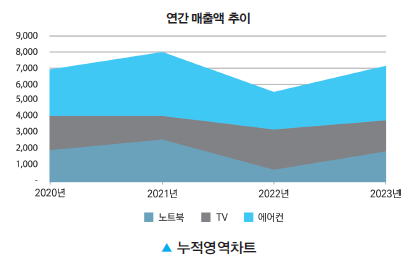
(6) 누적연속그래프(누적영역차트)
시간 변화에 따른 값의 변화를 선그래프의 영역으로 표현한다. 가로축은 시간을 나타내며 세로축은 데이터 값을 표시한다.
- 누적막대그래프와 유사하지만, 시간에 따라 변화하는 값의 흐름을 더 잘 보여준다. 또한, 세로 영역의 한 단면만 보여주면 그 시점의 분포를 볼 수 있다.
- 누적영역차트는 아래 부분의 데이터 값이 윗부분의 위치에 영향을 주기 때문에(값이 누적됨), 값의 분포를 표현하는 데 적합하며 한 집단의 경향성을 알아보기는 어렵다.